（1）为什么加深网络而不是加宽网络？

（2）说一下Focal loss ，Smooth-L1 loss

（3）RNN 为什么不便于处于长依赖序列（LSTM）

（4）减参卷积方式

为什么加深网络而不是加宽网络？

答：变宽模型仅仅是增加了同一层的计算单元，并未添加新的非线性拟合能力，而变深增加了模型的复杂度。

而深度学习成功内部三要素：逐层拟合，层之间的特征变化，足够的模型复杂度。正是需要加深网络才能解决

说一下Focal loss

Focal loss主要是为了解决 one-stage 目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

对于二分类来说传统 CE loss：

$$CE(x)= \begin{cases} -log(y')& \text{y=1}\\ -log(1-y')& \text{y=0}\\ \end{cases}$$ $$Fl(x)= \begin{cases} -\alpha(1-y')^{\gamma}log(y')& \text{y=1}\\ -(1-\alpha)(y')^{\gamma}log(1-y')& \text{y=0}\\ \end{cases}$$

$\alpha$ 平衡因子，经验调参，设为 0.25。$\gamma$ 是让简单的样本产生的 loss 更小，设为 2 ，让困难样本的 loss 大一些更利于挖掘复杂样本。

类别不均衡本质上就是分类难度差异上的体现

Smooth-L1 loss

L2 loss 对离群点异常敏感，梯度值容易过大

L1 loss 当预测框与 GT 差距较小时候，梯度仍为 1 ，可能优化不动

$$SL_1(x)= \begin{cases} 0.5x^2& if |x| < 1 \\ |x-|0.5&otherwise\\ \end{cases}$$

RNN 为什么不便于处于长依赖序列（LSTM）

长时间序列，存在 梯度消失或爆炸问题，导致普通 RNN 无法回忆起久远记忆

LSTM 多出了输入门、输出门、遗忘门，一条主线。

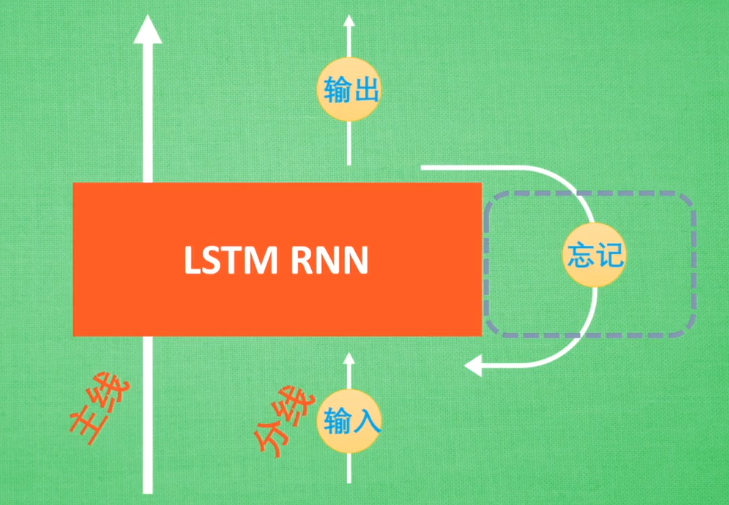
• 遗忘门：先前和当下的输入到细胞单元，使用 sigmoid 函数判断是否保留。决定从“细胞状态”中丢弃什么信息

  $f_t = \sigma(W([h_{t-1},x_t] + b)) $

• 输入门：更新单元状态，先决定哪些数据需要更新。决定放什么信息到“细胞状态”中

  $i_t = \sigma(W([h_{t-1},x_t] + b)) $ 新学的东西哪些要记住

  $\hat{C_t} = tanh(W([h_{t-1},x_t] + b))$ 新学的东西

  ${C_t} = f_t \times C_{t-1} + i_t \times \hat{C_t}$ 更新单元状态

• 输出门：先判断细胞状态的哪一部分输出，接着用 tanh 处理细胞状态

  $ o_t = \sigma {(W[h_{t-1},x_t] + b)}$

  $h_t = o_t \times tanh(C_T)$

sigmoid 函数 判断重要不重要，tanh 函数映射到 -1 到 1之间，再与

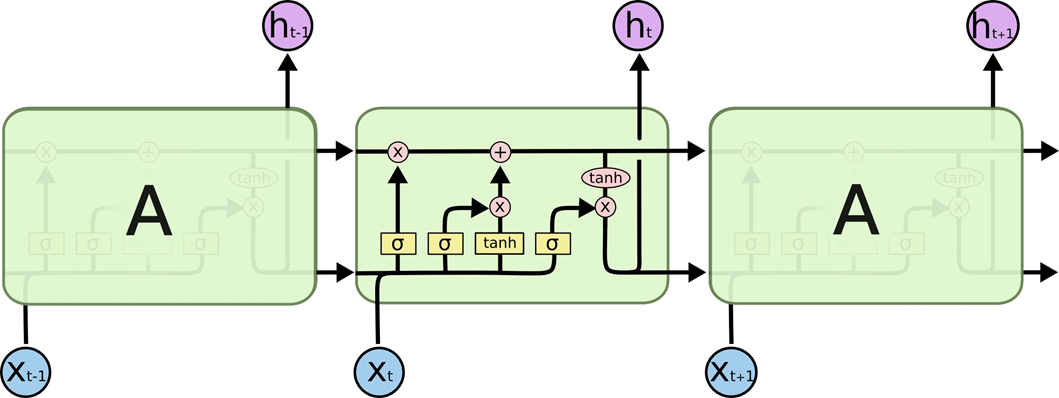
LSTM 为什么减轻了梯度消失问题

RNN 更新单元状态是连乘 $S_t = f(S_{t-1},x_t)$ 而 LSTM 更新单元格状态是 $S_t = \sum$， 一个连乘一个相加。

什么是分组卷积 ？为什么参数量会减少 ？

第一个问题

• 假设输入 feature map 是 $H \times W \times C $, 将 $C$ 分为 $g$ 组，每组尺寸为 $H \times W \times (C/g)$

• kernel 分为 $g$ 组，每组尺寸为 $h \times w \times (c/g)$

• 每组的 feature 与 kernel 做卷积，输出 $g$ 组 $H’ \times W’\times(k/g)$

第二个问题

假设输出 $c_1$ 通道输入，$c_2$ 通道输出

• 传统卷积 参数量为: $h \times w \times c_2 \times c_1$

• $h \times w \times(c1/g) \times (c2/g) \times g = \frac{1}{g} \times w \times c_1 \times c_2$

什么是深度可分离卷积

普通卷积：

• $N \times H \times W \times C$ 的输入，有 $k$ 个 3 \times 3 的 卷积，每个卷积核 $k_i$ 都要对 每个通道的 特征向量 $f_i$ 矩阵相乘后求和 $\sum_i^C (k_i \times f_i )$

深度可分离卷积：

• $N \times H \times W \times C$ 的输入分为 $C$ 组，每一个通道上都要做$ 3 \times 3 $的卷积，收集了每个通道上的空间特征
• 然后在做 $k$ 个 $ 1 \times 1$ 的卷积，收集每个点的特征并进行维度的扩增

参数对比 ( 3 通道输入，256 输出)：

• 普通卷积 3x3 Conv+BN+ReLU

  参数量：$ 3 \times 3 \times 3 \times 256 = 6912$

• Depthwise-pointwise 卷积 3x3 Depthwise Conv+BN+ReLU 和 1x1 Pointwise Conv+BN+ReLU

  参数量：$3 \times 3 \times 3 + 3 \times 1 \times 1 \times 256 = 795$